먼저 들어간 것이 나중에 나온다 - 후입선출(LIFO)
ADT - pust, pop, pick
void StackInt(Stack *pstack);
- 스택 초기화 진행
- 스택 생성 후에 가장 먼저 호출되어야 하는 함수임.
int isEmpty(Stack * pstack);
- 스택이 비어있는 유무에 따라서 bool값(0or1) 리턴
void push(Stack * pstack, Data data)
- 스택에 데이터 저장.
Data pop(Stack * pstack);
- 마지막에 저장된 요소 삭제, 삭제된 데이터는 반환- 이 함수의 호출을 위해서는 데이터가 하나 이상 꼭 존재해야함
Data Peek(Stack *pstack);
- 마지막에 저장된 요소를 반환하나 삭제는 안함- 얘도 마찬가지로 데이터가 하나 이상 존재함이 보장되어야 함.
중요한 것은... 스택은 두가지 방법으로 구현할 수 있음 . 첫번째는 배열을 기반으로, 두번째는 연결 리스트 기반으로 구현하는 것임. 당연히 둘다 할 수 있어야하고 상황에 따라서 더 적합한 방법을 선택해서 구현하면 됨.
1. 배열 기반
주의해야할 점 : 인덱스 0의 배열 요소가 스택의 바닥으로 정의된 점(인덱스 0의 요소를 바닥으로 정의하면 배열의 길이에 상관 없이 언제나 인덱스 0의 요소가 스택의 바닥이 되기 때문에), 마지막에 저장된 데이터의 위치를 기억하자. 가장 위에 저장된 데이터를 Top으로 가리키고 그 값을 변수에 저장함. 간단하게 정리해보면......... push는 Top을 위로 한칸 올리고, Top이 가리키는 위치에 데이터를 저장한다.pop은 Top이 가리키는 데이터를 반환하고 Top을 아래로 한 칸 내린다.
package stack_self;
public class Array implements Stack {
private int top_index;
private int stackSize;
private char dataArray[];
public Array(int stackSize) {
top_index = -1;
this.stackSize = stackSize;
dataArray = new char[this.stackSize]; //스택 사이즈와 같은 char형 배열을 만든다.
}
public boolean isEmpty() {
return (top_index == -1); //top의 인덱스가 -1이면 empty = 스택이 비어있다면
}
public boolean isFull() {
return (top_index == this.stackSize - 1);
}
public void push(char data) {
if(isFull()) System.out.println("Fail. Array Stack is Full");
else {
dataArray[++top_index] = data; //전치 연산자임을 주의! 데이터 추가를 위한 인덱스 값 증가
System.out.println("Inserted Data : " + data);
}
}
public char pop() {
if(isEmpty()) {
System.out.println("Fail. Array Stack is Empty");
return 'F';
}
else {
return dataArray[top_index--]; //삭제된 데이터를 반환
}
}
public void delete() { //삭제하는 함수
if(isEmpty()) System.out.println("Fail. Array Stack is Empty");
else {
top_index--; //pop 연산의 결과로 top_index값 하나 감소
}
}
public char peek() { //top 요소 반환
if(isEmpty()) {
System.out.println("Fail. Array Stack is Empty");
return 'F';
}
else {
return dataArray[top_index]; //맨 위에 저장된 데이터 반환
}
}
public void print() {
if(isEmpty()) System.out.println("Empty");
else {
System.out.printf("Array Stack: ");
for(int i = 0; i <= top_index; i++)
System.out.printf("%c", dataArray[i]);
System.out.println(); System.out.println();
}
}
}
2. 연결 리스트 기반
*스택도 연결 리스트임. 하지만!! 저장된 순서의 역순으로 조회 및 삭제가 가능함. 메모리 구조만 보면 단순한 연결 리스트와 구분이 가지 않지만, push와 pop이 포함된 ADT를 갖는다면 스택인 것임.
push : 리스트 마지막에 노드 삽입
pop : 리스트 마지막 노드 삭제
package stack_self;
public class Main01 {
public static void main(String[] args) {
int stackSize = 5;
char deletedData;
LinkedStack L = new LinkedStack();
/*
L.push('A');
L.push('B');
L.push('C');
L.print();
*/
char[] alphabets = new char[26];
for(int i = 0, num = 65; i < alphabets.length; i++, num++) {
alphabets[i] = (char)num;
L.push(alphabets[i]);
}
char ch = 'A';
for(int i = 0; i < alphabets.length; i++) {
alphabets[i] = ch++;
L.pop();
}
L.print();
}
}package stack_self;
class SNode{
char data;
SNode link;
}
class LinkedStack implements Stack{
private SNode top;
public boolean isEmpty() {
return (top == null);
}
public void push(char item) {
SNode newNode = new SNode();
/*
* newNode의 link를 top에 줘서...top으로 만드는거임ㅇㅋ?
*/
newNode.data = item;
newNode.link = top;
top = newNode;
System.out.println("Inserted item : " + item);
}
public char pop() {
if(isEmpty()) {
System.out.println("Fail. Empty");
return 'F';
}
else {
char item = top.data;
top = top.link;
return item;
}
}
public void delete() {
if(isEmpty()) System.out.println("Fail. Empty");
else {
top = top.link;
}
}
public char peek() {
if(isEmpty()) {
System.out.println("Fail. Empty");
return 'F';
}
else {
return top.data;
}
}
public void print() {
if(isEmpty()) System.out.println("Empty");
else {
SNode tmp = top;
System.out.println("Linked Stack: ");
while(tmp != null) {
System.out.printf("%c ", tmp.data);
tmp = tmp.link;
}
System.out.println();
}
}
}
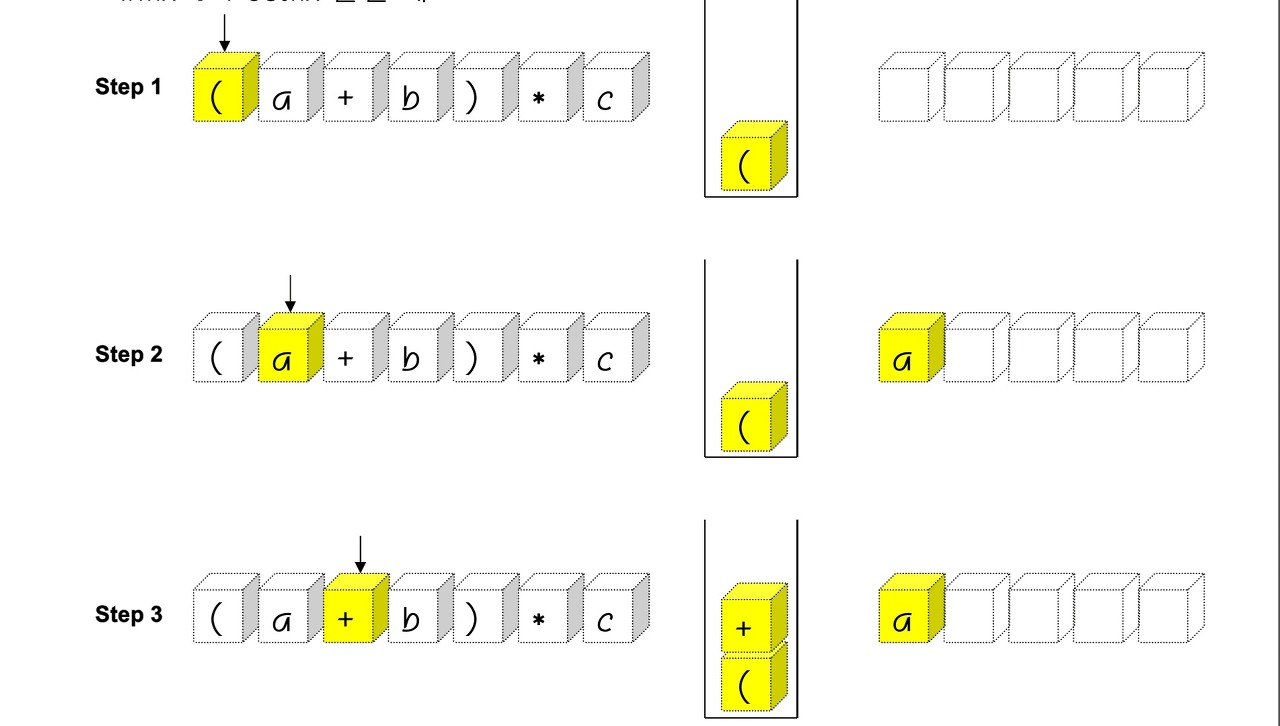
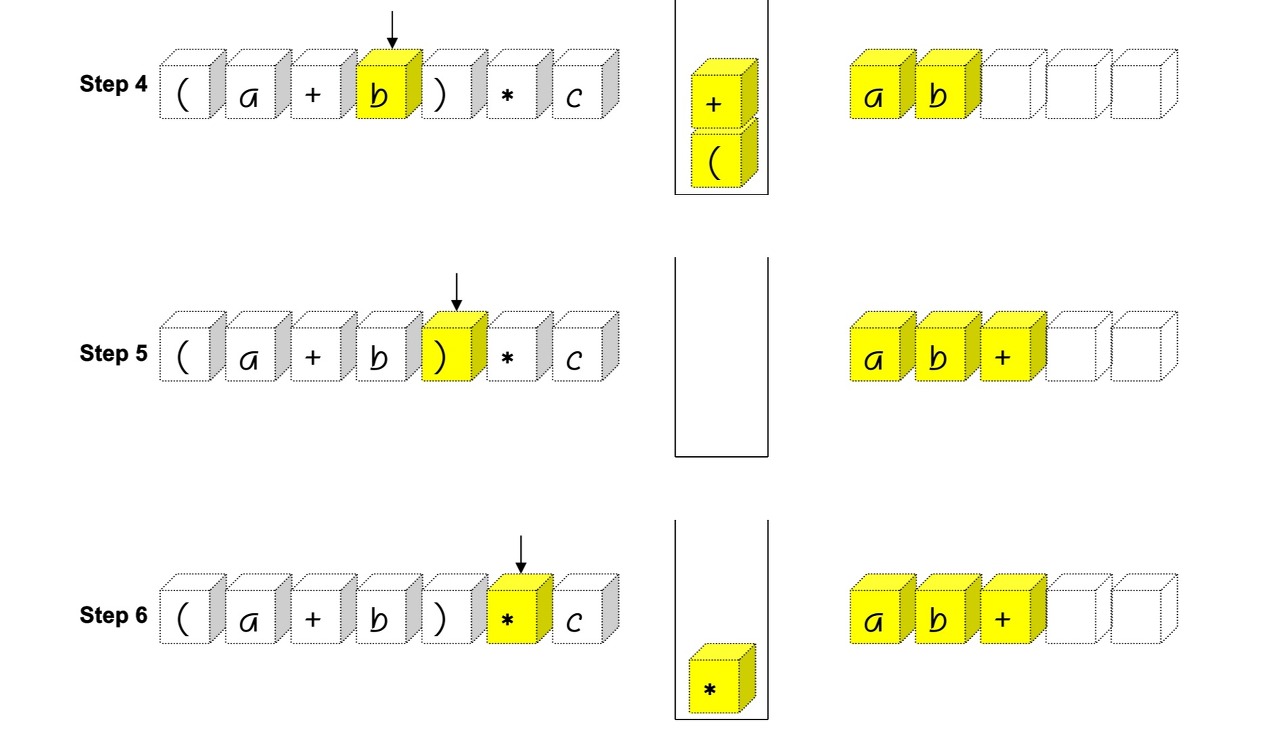
Infix to Postfix 알고리즘 (with swich문, stack)
피연산자의 순서가 동일하고 연산자들의 순서만 다르다. 왜냐? 연산자만 스택에 저장하니까.
ex) 3+4*5 -> 345*+
피연산자 만나면 그대로 출력,
연산자 만나면 스택에 저장했다가 스택보다 우선 순위가 낮은 연산자가 나올 시 출력
왼쪽 괄호는 우선 순위가 가장 낮음.
오른쪽 괄호가 나오면 스택에서 왼쪽 괄호 위에 쌓여있는 모든 연산자 출력.

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
|
package stack_self;
//괄호를 가진 임의의 수식을 입력하여 괄호의 짝이 맞는지 검사
public class ValidBraces {
private String exp; //exp = expression(수식)
private int expSize; //수식의 size
private char test, openPair;
/*
* 1.괄호 검사 하는 boolean 메소드
* 수식을 왼->오 방향으로 하나씩 스캔한다.
* 왼쪽 괄호를 만나면 스택에 push
* 오른쪽 괄호를 만나면 스택에 pop해서 마지막에 저장한 괄호와 같은지 확인(bool)
* 검사가 다 끝났을 때 공백 스택이 되어야함.
* 만약 공백이 되지 않으면 괄호 개수가 틀린 수식임
*/
public boolean is_Valid_Braces(String exp) {
this.exp = exp;
expSize = this.exp.length();
LinkedStack S = new LinkedStack();
for(int i = 0; i <expSize; i++) { //수식의 사이즈만큼 스캔한다
test = this.exp.charAt(i);
switch(test) {
case '(':
case '[':
case '{':
S.push(test); break;
case ')':
case ']':
case '}':
if(S.isEmpty()) return false;
else {
openPair = S.pop();
if( (openPair == '(' && test != ')')||
(openPair == '[' && test != ']')||
(openPair == '{' && test != '}'))
return false;
else break;
}
default:
}
}
if(S.isEmpty()) return true;
else return false;
}
/*
* Infix to Postfix 알고리즘
* 피연산자의 순서가 동일하고 연산자들의 순서만 다르다. 왜냐? 연산자만 스택에 저장하니까.
* ex) 3+4*5 -> 345*+
* 피연산자 만나면 그대로 출력,
* 연산자 만나면 스택에 저장했다가 스택보다 우선 순위가 낮은 연산자가 나올 시 출력
* 왼쪽 괄호는 우선 순위가 가장 낮음.
* 오른쪽 괄호가 나오면 스택에서 왼쪽 괄호 위에 쌓여있는 모든 연산자 출력.
*/
public char[] infix_to_postfix(String infix) {
int infixSize = infix.length(); //infix: 익숙한 형태의 그 수식
char postfix[] = new char[infixSize];
int j = 0;
LinkedStack S = new LinkedStack();
for(int i = 0; i < expSize; i++) {
char tmp = this.exp.charAt(i);
switch (tmp) {
//피연산자부터.
case '0' :
case '1' :
case '2' :
case '3' :
case '4' :
case '5' :
case '6' :
case '7' :
case '8' :
case '9' :
postfix[j++] = tmp; break; //결과(postfix)에 차례대로 넣어준다.
//연산자는 스택에 push 해준다.
case '+' :
case '-' :
case '*' :
case '/' :
S.push(tmp); break;
case ')':
postfix[j++] = S.pop(); break; //pop은 item을 리턴
case'\0': //null 문자 , 문자열의 끝을 나타냄.
while(S.isEmpty() != true) postfix[j++] = S.pop();
break;
default:
}
}
return postfix;
}
}
|
cs |
'Major > Data Structure & Algorithm' 카테고리의 다른 글
| Binary Tree (0) | 2022.05.22 |
|---|---|
| 후위식 연산 (0) | 2022.04.22 |
| review (0) | 2022.04.16 |
| 원형 연결 리스트 (0) | 2022.04.16 |
| 이중 연결 리스트의 삽입, 삭제 + (다항식 연산 ) (0) | 2022.04.13 |
